
In effect, we are dividing the atom into very thin concentric shells, much like the layers of an onion ( Figure 3.6.1a), and calculating the probability of finding an electron on each spherical shell.
#Atomic orbitals quantum numbers series
In contrast, we can calculate the radial probability (the probability of finding a 1s electron at a distance r from the nucleus) by adding together the probabilities of an electron being at all points on a series of x spherical shells of radius r 1, r 2, r 3,…, r x-1, r x. At very large values of r, the electron probability density is very small but not zero. The probability density is greatest at r = 0 (at the nucleus) and decreases steadily with increasing distance. The 1 s orbital is spherically symmetrical, so the probability of finding a 1 s electron at any given point depends only on its distance from the nucleus. Because \Psi^2 gives the probability of finding an electron in a given volume of space (such as a cubic picometer), a plot of \Psi^2 versus distance from the nucleus ( r) is a plot of the probability density. One way of representing electron probability distributions was illustrated previously for the orbital of hydrogen.
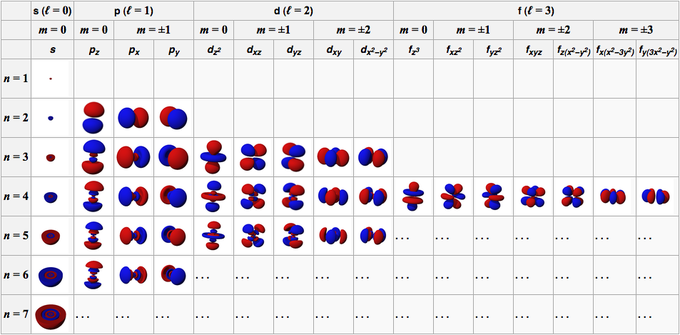
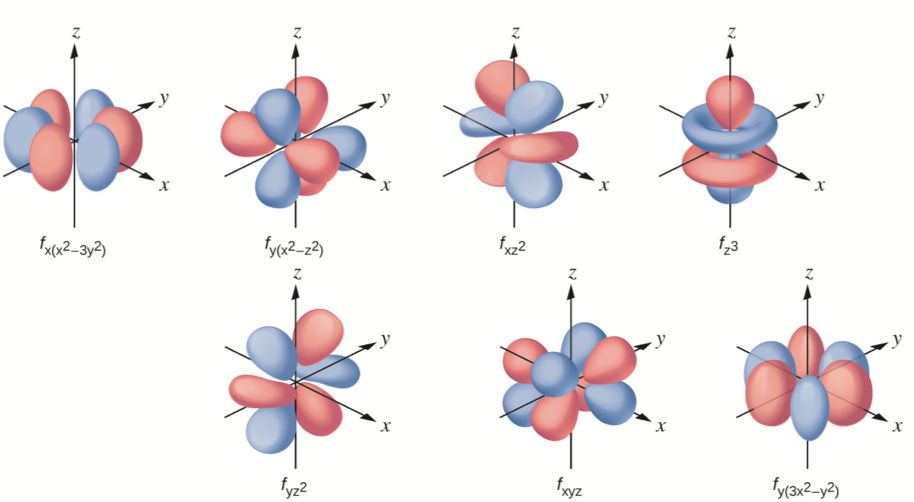
In contrast to his concept of a simple circular orbit with a fixed radius, orbitals are mathematically derived regions of space with different probabilities of containing an electron. To understand the 3D representation of electronic orbitalsĪn orbital is the quantum mechanical refinement of Bohr’s orbit.List and describe traits of the four quantum numbers that form the basis for completely specifying the state of an electron in an atom.Understand the general idea of the quantum mechanical description of electrons in an atom, and that it uses the notion of three-dimensional wave functions, or orbitals, that define the distribution of probability to find an electron in a particular part of space.


 0 kommentar(er)
0 kommentar(er)
